
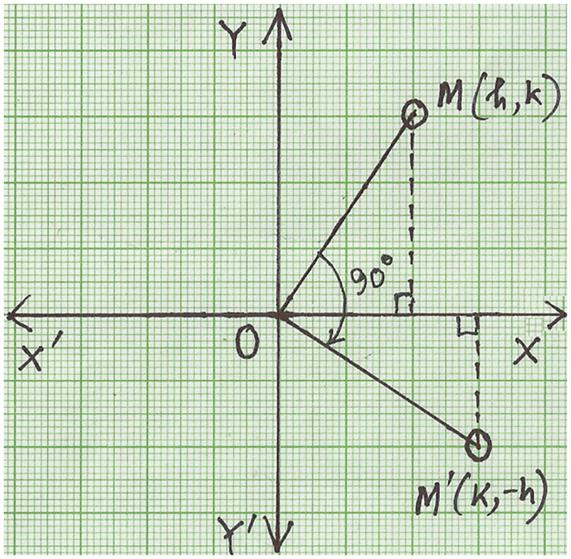
Hence, with change of coordinate from P (h, k) to P (k,-h) we can rotation a figure 90. Describe the rotational transformation that maps after two successive reflections over intersecting lines. Rotate a figure 90 clockwise about a point : When a point say P (h, k) is rotated about origin O through 90 clockwise direction, the new position will be P (k,-h) Since to rotate 90 clockwise about a point, every point x, y will rotate to y,-x.How are they related New Resources Banca Boat (version 2) Graphing Perpendicular Lines in the Coordinate Plane Chapter-01: Example 1.1 mirkasophia Colorful Egg (Pisanka) Discover Resources CCGPS AG 1.3. Describe and graph rotational symmetry. Click and drag the blue dot to see it's image after a 90 degree clockwise rotation (the green dot).

In the video that follows, you’ll look at how to: The order of rotations is the number of times we can turn the object to create symmetry, and the magnitude of rotations is the angle in degree for each turn, as nicely stated by Math Bits Notebook.
Example 01 The point (3, 4) is rotated 90 degree counterclockwise around origin. And when describing rotational symmetry, it is always helpful to identify the order of rotations and the magnitude of rotations. If point (h, k) is rotated 90 degree counterclockwise, then the final position of point will be (-k, h) Hence, If original point (h, k) then 90 degree counterclockwise rotated point (-k, h) Let us see some solved examples for further understanding. Rotating 90 degrees Clockwise Click and drag the blue dot to see its image after a 90 degree clockwise rotation (the green dot). This means that if we turn an object 180° or less, the new image will look the same as the original preimage. Rule of 90 Degree Rotation about the Origin When the object is rotating towards 90 clockwise then the given point will change from (x,y) to (y,-x). In short, switch x and y and make x negative. Lastly, a figure in a plane has rotational symmetry if the figure can be mapped onto itself by a rotation of 180° or less. 90 Degree Clockwise Rotation If a point is rotating 90 degrees clockwise about the origin our point M (x,y) becomes M' (y,-x).


 0 kommentar(er)
0 kommentar(er)
